Introduction to Michaelis-Menten Kinetics

July 22, 2020 ☼ Molecular Biology ☼ Programming

One of the fundamental topics that students learn in their introductory biology or biochemistry classes is enzyme kinetics. Enzyme kinetics is the study of how enzymes interact with their target substrate and turn it over into the final product. This field includes studying the rate that substrates are turned over, the specificity of the enzyme, and so much more. Within this field, one of the critical mathematical models that underpin much of the literature and our understanding of enzymes is the Michaelis-Menten model.

Table of Contents

1. Model Background
2. Mathematical Derivation
3. Additional Constant: Enzyme Efficiency
4. Interactive Exploration
5. Closing

Model Background

The Michaelis-Menten model describes the process of an enzyme-catalyzed reaction consisting of a single enzyme (E) catalyzing the conversion of a substrate (S) to a final product (P). We can represent this process as the following chemical reaction:

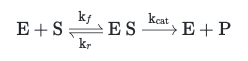Michaelis-Menten Reaction Model

This representation introduces one new molecular species (in addition to the three above) and three rate constants:

• ES: Intermediate enzyme-substrate complex
• $k_f$: Forward rate constant to describe the association of E and S
• $k_r$: Reverse rate constant to describe the dissociation of ES
• $k_{cat}$: Catalytic rate constant (turnover rate) to describe the conversion of substrate to product per unit time.

Model Assumptions

To use this model of an enzyme-catalyzed reaction, we are required to make a series of assumptions about the system:

1. The reverse reaction from product to substrate is ignored
2. $\frac{d[ES]}{dt} = 0$
3. [S] is approximately constant through the duration of the reaction

Assumption 2 (the steady-state assumption) comes from assuming that $k_{cat} \ll k_f$ and $k_{cat} \ll k_r$. In other words, the binding and unbinding events between the substrate and free enzyme can regenerate ES complexes faster than they are turned over to generate free enzyme and product. This assumption enables us to solve a system of differential equations (See Mathematical Derivation below).

Assumption 3 comes from assuming [S] is in excess compared to [E]. In other words, the formation of ES results in negligible changes to the [S].

With these assumptions in mind, let’s walk through the mathematical derivation.

Mathematical Derivation

While understanding the mathematical derivation of the Michaelis-Menten model is not essential for practical applications, it enables you to understand precisely how the model works.

We start by setting up differential equations to describe the change in concentrations for each species:

$$\frac{d[E]}{dt} = -k_f[E][S] + k_r[ES] + k_{cat}[ES] \tag{1}$$

$$\frac{d[S]}{dt} = -k_f[E][S] + k_r[ES] \tag{2}$$

$$\frac{d[ES]}{dt} = k_f[E][S] - k_r[ES] - k_{cat}[ES] \tag{3}$$

$$\frac{d[P]}{dt} = v = k_{cat}[ES] \tag{4}$$

Using the steady-state assumption (Assumption 2), we simplify 3 to the following:

$$\frac{[E][S]}{[ES]} = \frac{k_r + k_{cat}}{k_f} \tag{5}$$

Here, we define one of the key constants for describing enzymes, the Michaelis-Menten Constant:

$$\text{K}_m = \frac{k_r + k_{cat}}{k_f} \tag{6}$$

From this mathematical interpretation, the Michaelis-Menten constant appears to be a ratio of the dissociation/transformation and the formation of the ES complex. Importantly, this constant is not dependent on the concentrations of any of the components, meaning it’s an inherent characteristic of the enzyme-substrate interaction itself.

Now, we plug in our definition of $\text{K}m$ into (5), and after some algebraic manipulation, plug in the resulting equation into (4):

$$v = \frac{k_{cat}[E][S]}{_m} \tag{7}$$

This transformation is important because it shifts the dependence on [ES], a quantity that is difficult to measure, to [E] and [S]. While [S] is now a quantity that we can control, we now need to remove the dependence on [E].

To remove this dependence, we define two additional equations:

$$V_{max} = k_{cat}[E]_{tot} \tag{8}$$

$$E_{tot} = [E] + [E S] \tag{9}$$

(8) represents the upper product formation rate when all enzymes are saturated with substrate. (9) comes from the conservation of mass.

We know combine (8) and (9):

$$V_{max} = k_{cat}[E] + k_{cat}[ES] \tag{10}$$

Using the same manipulation to generate (7) and some algebraic manipulation, we can determine an equation to describe $K_{cat}[E]$:

$$K_{cat}[E] = \frac{V_{max}}{1 + } \tag{11}$$

Plugging (11) back into (7) and simplifying the resultant equation, we get the final form of the Michaelis-Menten Model:

$$v = \frac{V_{max}[S]}{K_m + [S]}$$

A plot of this equation shows the characteristic Michaelis-Menten curve that describes the initial velocity for a given [S]. As expected, the curve increases rapidly at low [S], but eventually saturates at $V_{max}$.

Back to $K_m$

Earlier when I introduced $K_m$, I mentioned that it has a special meaning. To illustrate what this is, let’s solve for the substrate concentration when $v = \frac{V_{max}}{2}$.

$$\frac{V_{max}}{2} = \frac{V_{max}[S]}{K_m + [S]}$$

From this equation, you may see that this equation is true when $K_m = [S]$, giving us an experimental interpretation of $K_m$:

$K_m$ is the substrate concentration at which the reaction is proceeding at half the maximal velocity. In other words, $K_m$ is a measure of how sensitive an enzyme is to the substrate. If the $K_m$ is small, the reaction rate quickly saturates even at low substrate concentrations. If $K_m$ is large, then the reaction may only be meaningful at high substrate concentrations. To illustrate this relationship, let’s compare the plots of multiple $K_m$ values:

Additional Constant: Enzyme Efficiency

One final constant that comes from the Michaelis-Menten kinetics model is the Efficiency Constant:

$$\text{Efficiency Constant} = \frac{k_{cat}}{K_m}$$

This constant captures how well an enzyme catalyzes a reaction through the two key contributors:

1. How fast the enzyme turns over substrate to product
2. How well the enzyme binds the substrate.

For example, if the enzyme has a high turnover rate (Large $k_{cat}$), the efficiency constant will be high. Additionally, if the enzyme binds the substrate strongly (Small $K_m$), the efficiency rate will also be high.

Interactive Exploration

While seeing the mathematical derivation and static graphs is helpful, the best way to explore the effects of changing the two parameters, $K_m$ and $V_{max}$, is to play around with them directly. Below, there are links to a Python notebook that provides an environment to explore the model in more detail.

Closing

Michaelis-Menten kinetics is one of the fundamental models underpinning our understanding of enzymology. I hope this post demystified the mathematics behind the model, and the interactive Python notebook provided a conducive environment for furthering your understanding of each of the main parameters.